Галина Григорьева
Мастер-класс для воспитателей «Использование кругов Эйлера для развития логического мышления дошкольников»
Тема нашего мастер класса «Использование кругов Эйлера для развития логического мышления дошкольников».(слайд 1)
Круги Эйлера были изобретены Леонардом Эйлером в 18 веке. Леонард Эйлер — швейцарский, немецкий и российский математик и механик 18 века. Написал более 850 научных работ. В одной из них и появились круги Эйлера. (слайд 2)
С тех пор круги Эйлера широко используются в математике, логике.
Публикация «Мастер-класс для воспитателей „Использование кругов Эйлера для развития логического мышления дошкольников“» размещена в разделах
- Логическое мышление
- Мастер-классы для воспитателей и педагогов
- Методические материалы для педагогов и воспитателей
- Множества
- Работа. Педсоветы, семинары, тренинги для педагогов
- Развитие ребенка. Материалы для педагогов
- Темочки
Круги Эйлера можно использовать как в различных образовательных областях "Речевое развитие", "Познавательное развитие", "Социально – коммуникативное развитие», «Художественно-эстетическое развитие», «Физическое развитие», так и в самостоятельной деятельности детей.
(слайд 3)
Используя круги Эйлера ребенок учится сопоставлять, обобщать, группировать материал, развивается речь, память и мышление.
Построение и использование наглядных моделей способствует развитию умственных способностей дошкольников. (слайд 4)
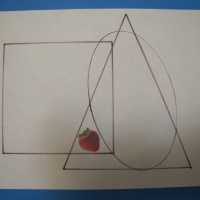
Круги Эйлера - это геометрическая схема, с помощью которой можно наглядно отобразить отношения между понятиями или множествами объектов.
Существуют несколько моделей кругов:
а) Непересекающиеся круги;
б) Пересекающиеся круги;
в) Один круг вложен в другой (слайд 5)
Дидактический материал для игр с обручами.
Обручи.
Плоскостные круги и ковролин.
Карточки с изображением предметов (подобные картинному лото).
Кодовые карточки.
Карточки со знаком отрицания.
Различные мелкие предметы.
Блоки Дьенеша. (слайд 6)
Целесообразно использовать кодовые карточки, т. е графические условные знаки знакового обозначения свойств предметов (Слайд 7)
Когда дети свободно научаться пользоваться кодовыми карточками вводится код, обозначающий знак отрицания «НЕ», который в рисуночном коде выражается перечеркиванием крест – накрест соответствующего кодирующего рисунка. (слайд 8)
Работа по обучению разделения на множества и подмножества должна идти в несколько этапов, с постепенным усложнением.
Начать применять данную технологию можно с детьми младшего возраста. Для начала вы им объясняете, что означает «положить в круг, обруч», и что такое «положить предмет вне круга»
Игра «Разложи, не спеши»
Цель: закрепление понятий «внутри круга», «вне круга»
Ход игры: Раскладывается круг красного цвета. Дети располагают все большие фигуры внутри круга, а все маленькие фигуры «вне» красного круга. В синем кругу все желтые предметы, красные «вне круга»(слайд9)
Затем можно приступать к распределению предметов на 2 круга. По мере усвоения материала задания постепенно усложняются. В средней группе используются уже два не пересекающихся обруча
Игра «Разложи по цвету»
Цель: формирование операций классификации по одному признаку, развитие логического мышления.
Ход игры: Круги раскладываются, не пересекаясь. В желтый круг дети помещают все фигуры жёлтого цвета, в красный – все фигуры красного цвета. (слайд 10)
В старшем возрасте предлагаются игры и упражнения двумя пересекающимися обручами.
Например: Задание «У вас есть картинки, положите пожалуйста в один круг только желтые предметы а в другой круг транспорт».
В данном положении может возникнуть спор у детей, т. к. желтый автомобиль может оказаться и в том и другом круге., множестве
Здесь, важно дать время детям подумать, обсудить, поспорить между собой. И придумать решение. Хорошо, если кто то догадается положить желтую машину по середине, а может быть кто то сделает открытие и догадается пересечь круги и тогда желтая машина окажется в обоих кругах сразу. Именно вот эта зона будет называться пересечение множеств. Такие пересекаемые множества могут быть в том случае, если мы возьмем разные типы признаков: форма, цвет, величина, размер(слайд 11.12,13)
Символы с отрицанием. Учим детей понимать символы отрицания, например : не желтый, не круглый
В один круг кладем предметы не желтые, в другой не круглые. Что положить на пересечение?
Красные - не круглые. Задание на первый взгляд может показаться сложным, но если выполнять последовательно, то все получается красиво.
По мере усвоения материала задания усложняются (слайд 14)
Модель кругов Эйлера один круг вложен в другой, позволяет научить детей классифицировать окружающий мир по признакам, свойствам, принадлежности и т. д.
На большой круг кладут картинки представителей животного мира вперемешку
Далее, Дети берут в руки все картинки и раскладывают в круги меньших размеров, которые располагаются в большом круге: (цвет кругов определяете сами) в
В зеленый животных леса, желтый – домашних, голубой – животных жарких стран.
В эти круги можно вносить не только животных, а что и кого угодно, только нужно сохранять основной принцип: в большом круге располагаются элементы, у которых одинаковые признаки, принадлежность, свойства, а в маленьком располагаются элементы с такими же признаками, свойствами, принадлежностью, но они должны объединяться каким то отличительной особенностью
В нашем случае: одинаковый признак– животные, разные принадлежности, животные леса, домашние и жарких стран. (слайд 15)
В подготовительной группе вводятся более сложные игры и упражнения с использованием уже трех пересекающихся между собой обручей. .(слайд 16)
Еще предлагаю познакомиться с игрой с пересекающимися кругами Эйлера (слайд 16)
Такую игру можно предложить не только старшим дошкольникам, но и родителям на собраниях.
Вы предлагаете взять три круга. В каждый круг положить разные типы признаков : квадратный, маленький, красный. (форма, размер, цвет)
Возьмем блоки Дьенеша 24 фигурок.
Задача: нужно разложить все 24 фигур с помощью наших заданий. Время 1 мин.
Напомню, чтобы решить эту задачу, нужно делать все последовательно.
Проверка:
1-все квадратные фигуры, большие и маленькие, и красные. Все оказываются здесь
2- выбираем маленькие из оставшихся за кругом, кладем во второй круг. На 1 круг не смотрим
3- из оставшихся выбираем красные, кладем в 3 круг. Некоторые фигуры остаются в 8 зоне
Когда мы разложили последовательно все по множествам, можно раскладывать на пересечения. Квадратные – маленькие, ищем везде маленькие квадраты и раскладываем в пересечение 4
Маленькие красные – оказываются на пересечении 5
Красные квадраты – оказываются на пересечении 6
А в середине 7 пересечение – маленький, красный, квадрат.
Красота! Решили сложнейшую задачу, рассуждая последовательно, такая задача доступна каждому ребенку в подготовительной группе.
Предлагаю вам немного поиграть и понять, как же можно применять данную технологию в практике с детьми.
Играем с помощью модели кругов «Один круг вложен в другой»
Наш большой круг это все животные. У каждого у вас есть своя карточка, внимательно рассмотрите ее, нужно Найти и разложить (т. е встать с карточкой) всех животных по месту обитания. Обителей леса, Обитатели севера, обитатели жарких стран. Если у вас карточки не подходят ни к одному классу, то оставляем за кругом.
(карточки: обитатели леса, обитатели севера, обитатели жарких стран, насекомые)
Галина Григорьева | Все публикации
