![]() Лилия Искакова
Лилия Искакова
О структуре логического мышления у старших дошкольников
▼ Скачать + Заказать документы
О структуре логического мышления
Аннотация. В статье приводится структура логического мышления, уточняются его характеристики. Каждый элемент кратко характеризуется и иллюстрируется с помощью примеров на математическом содержании. Показывается целесообразность формирования логического мышления именно на начальном уровне образования.
Темочки:
- Логическое мышление
- Старшая группа
- Темочки
- Конкурс для воспитателей и педагогов «Лучшая методическая разработка» декабрь 2024
Ключевые слова: логическое мышление, элементы логического мышления, формы логического мышления, структура логического мышления.
Владение логическим мышлением позволяет человеку решать проблемы как в профессиональной, так и в повседневной деятельности. Однако такое мышление не является чем-то данным от природы, процесс его формирования сложен и длителен. Наиболее интенсивно логическое мышление формируется в младшем школьном возрасте. Именно поэтому в федеральном государственном образовательном стандарте начального общего образования декларируются требования к условиям его формирования, а в качестве обязательных образовательных результатов заявлены базовые логические действия как подгруппа познавательных универсальных учебных действий. Между тем, базовые логические действия являются лишь одним из компонентов логического мышления, поэтому для целенаправленного его формирования у младших школьников целесообразно рассмотреть его полную структуру.
В научных источниках логическое мышление, в силу его многогранности и многоаспектности, определяется по-разному. Так, в Словаре-справочнике по возрастной и педагогической психологии под логическим мышлением понимается «один из видов мышления, характеризующийся использованием понятий, логических конструкций» [3]. Из приведенного определения следует, что такое мышление оперирует понятиями и силлогизмами (определенными структурами мышления, каковыми в логическом мышлении являются суждения и умозаключения).
В определении логического мышления, данном в словаре Современный образовательный процесс, основные понятия и термины как вида мышления, заключающегося в оперировании понятиями, суждениями и умозаключениями, перечисляются все формы, в которых такого рода мышление осуществляется [4].
А. А. Белик логическое мышление трактует как историческую форму мышления, опирающуюся на законы тождества, непротиворечивости в рассуждениях [1]. Здесь мы видим такую характеристику логического мышления, как непротиворечивость в рассуждениях.
А. А. Реан под логическим мышлением понимает вид мыслительного процесса, в котором используются логические конструкции и готовые понятия. [2].
Таким образом, сущность логического мышления заключается в следующем:
это владение совокупностью структур мышления, характеризующихся непротиворечивостью;
осуществляется в формах: понятие, суждение: умозаключение.
Коротко охарактеризуем названные формы.
Понятие – это слово (термин, которое объединяет класс объектов, обладающих некоторым набором признаков. Причем, этот набор присущ только этому классу объектов. Он называется содержанием понятия, а сам класс объектов – объемом понятия.
Пример математического понятия – прямоугольник. Этот термин объединяет все прямоугольники (например, начерченные на любой поверхности, вырезанные из какого-либо материала, существующие в представлении и т. п.). Содержанием понятия «прямоугольник» будет набор следующих признаков:
это плоская фигура,
стороны прямоугольника являются отрезками,
это многоугольник,
у него 4 вершины, 4 стороны,
это параллелограмм,
все углы прямые,
противоположные стороны равны,
противоположные стороны попарно параллельны,
диагонали прямоугольника равны.
Если из приведенного набора признаков выбрать необходимый и достаточный набор для распознавания прямоугольника среди других объектов, то получим определение этого понятия: «прямоугольник – это параллелограмм с прямым углом» или «прямоугольник – это четырехугольник, у которого все углы прямые».
Таким образом, над понятиями можно выполнять определенные операции, в частности, их определение, то есть формулирование набора признаков, необходимого и достаточного для распознавания этого понятия среди других объектов.
К операциям над понятиями относятся также следующие:
расширение (обобщение) понятий. Эта операция заключается в том, что из содержания понятия исключаются некоторые признаки. Так, если из содержания понятия «прямоугольник» удалить признак «углы прямые», то получим более широкое понятие «параллелограмм»;
сужение (конкретизация) понятий. Операция, обратная предыдущей. Например, добавив в содержание понятия «прямоугольник» признак «смежные стороны равны», получим более узкое понятие «квадрат» (частный случай прямоугольника);
установление отношений между понятиями. Например, отношение между понятиями «прямоугольник» и «квадрат» - родовидовые, где первое – родовое понятие, а второе – его вид.
Суждение – это повествовательное предложение, содержащее утверждение, о котором можно сказать, истинное оно или ложное. С помощью суждения связываются два понятия. Например, «квадрат – это прямоугольник». В нашем случае суждение является истинным. То есть
1 из 7
О структуре логического мышления
С. П. Зубова, Л. А. Искакова
Аннотация. В статье приводится структура логического мышления, уточняются его характеристики. Каждый элемент кратко характеризуется и иллюстрируется с помощью примеров на математическом содержании. Показывается целесообразность формирования логического мышления именно на начальном уровне образования.
Ключевые слова: логическое мышление, элементы логического мышления, формы логического мышления, структура логического мышления.
Владение логическим мышлением позволяет человеку решать проблемы как в профессиональной, так и в повседневной деятельности. Однако такое мышление не является чем-то данным от природы, процесс его формирования сложен и длителен. Наиболее интенсивно логическое мышление формируется в младшем школьном возрасте. Именно поэтому в федеральном государственном образовательном стандарте начального общего образования декларируются требования к условиям его формирования, а в качестве обязательных образовательных результатов заявлены базовые логические действия как подгруппа познавательных универсальных учебных действий. Между тем, базовые логические действия являются лишь одним из компонентов логического мышления, поэтому для целенаправленного его формирования у младших школьников целесообразно рассмотреть его полную структуру.
В научных источниках логическое мышление, в силу его многогранности и многоаспектности, определяется по-разному. Так, в Словаре-справочнике по возрастной и педагогической психологии под логическим мышлением понимается «один из видов мышления, характеризующийся использованием понятий, логических конструкций» [3]. Из приведенного определения следует, что такое мышление оперирует понятиями и силлогизмами (определенными структурами мышления, каковыми в логическом мышлении являются суждения и умозаключения).
2 из 7
В определении логического мышления, данном в словаре Современный образовательный процесс, основные понятия и термины как вида мышления, заключающегося в оперировании понятиями, суждениями и умозаключениями, перечисляются все формы, в которых такого рода мышление осуществляется [4].
А. А. Белик логическое мышление трактует как историческую форму мышления, опирающуюся на законы тождества, непротиворечивости в рассуждениях [1]. Здесь мы видим такую характеристику логического мышления, как непротиворечивость в рассуждениях.
А. А. Реан под логическим мышлением понимает вид мыслительного процесса, в котором используются логические конструкции и готовые понятия. [2].
Таким образом, сущность логического мышления заключается в следующем:
это владение совокупностью структур мышления, характеризующихся непротиворечивостью;
осуществляется в формах: понятие, суждение: умозаключение.
Коротко охарактеризуем названные формы.
Понятие – это слово (термин, которое объединяет класс объектов, обладающих некоторым набором признаков. Причем, этот набор присущ только этому классу объектов. Он называется содержанием понятия, а сам класс объектов – объемом понятия.
Пример математического понятия – прямоугольник. Этот термин объединяет все прямоугольники (например, начерченные на любой поверхности, вырезанные из какого-либо материала, существующие в представлении и т. п.). Содержанием понятия «прямоугольник» будет набор следующих признаков:
это плоская фигура,
стороны прямоугольника являются отрезками,
это многоугольник,
у него 4 вершины, 4 стороны,
3 из 7
это параллелограмм,
все углы прямые,
противоположные стороны равны,
противоположные стороны попарно параллельны,
диагонали прямоугольника равны.
Если из приведенного набора признаков выбрать необходимый и достаточный набор для распознавания прямоугольника среди других объектов, то получим определение этого понятия: «прямоугольник – это параллелограмм с прямым углом» или «прямоугольник – это четырехугольник, у которого все углы прямые».
Таким образом, над понятиями можно выполнять определенные операции, в частности, их определение, то есть формулирование набора признаков, необходимого и достаточного для распознавания этого понятия среди других объектов.
К операциям над понятиями относятся также следующие:
расширение (обобщение) понятий. Эта операция заключается в том, что из содержания понятия исключаются некоторые признаки. Так, если из содержания понятия «прямоугольник» удалить признак «углы прямые», то получим более широкое понятие «параллелограмм»;
сужение (конкретизация) понятий. Операция, обратная предыдущей. Например, добавив в содержание понятия «прямоугольник» признак «смежные стороны равны», получим более узкое понятие «квадрат» (частный случай прямоугольника);
установление отношений между понятиями. Например, отношение между понятиями «прямоугольник» и «квадрат» - родовидовые, где первое – родовое понятие, а второе – его вид.
Суждение – это повествовательное предложение, содержащее утверждение, о котором можно сказать, истинное оно или ложное. С помощью суждения связываются два понятия. Например, «квадрат – это прямоугольник». В нашем случае суждение является истинным. То есть
4 из 7
операция над суждениями заключается в установлении его истинности или ложности.
Умозаключение – это процедура перехода от одного суждения к другому. Так как суждения бывают единичными и общими, то и процедуры перехода от одного вида суждений различны.
Индукция – вид рассуждения от единичного к общему, она бывает полной (когда перебираются все единичные случаи и на основе сравнения этих случаев делается общий вывод относительно только этих случаев) и неполной (когда на основе перебора нескольких единичных суждений выявляется их сходство и делается общий вывод, фиксирующий это сходство, распространяющийся на все подобные случаи).
Приведем примеры полной и неполной индукции.
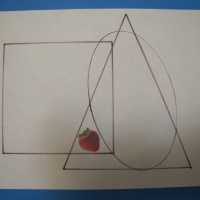
Как называется каждая из фигур? Дай общее название этим фигурам.
1 из 7
О структуре логического мышления
С. П. Зубова, Л. А. Искакова
Аннотация. В статье приводится структура логического мышления, уточняются его характеристики. Каждый элемент кратко характеризуется и иллюстрируется с помощью примеров на математическом содержании. Показывается целесообразность формирования логического мышления именно на начальном уровне образования.
Ключевые слова: логическое мышление, элементы логического мышления, формы логического мышления, структура логического мышления.
Владение логическим мышлением позволяет человеку решать проблемы как в профессиональной, так и в повседневной деятельности. Однако такое мышление не является чем-то данным от природы, процесс его формирования сложен и длителен. Наиболее интенсивно логическое мышление формируется в младшем школьном возрасте. Именно поэтому в федеральном государственном образовательном стандарте начального общего образования декларируются требования к условиям его формирования, а в качестве обязательных образовательных результатов заявлены базовые логические действия как подгруппа познавательных универсальных учебных действий. Между тем, базовые логические действия являются лишь одним из компонентов логического мышления, поэтому для целенаправленного его формирования у младших школьников целесообразно рассмотреть его полную структуру.
В научных источниках логическое мышление, в силу его многогранности и многоаспектности, определяется по-разному. Так, в Словаре-справочнике по возрастной и педагогической психологии под логическим мышлением понимается «один из видов мышления, характеризующийся использованием понятий, логических конструкций» [3]. Из приведенного определения следует, что такое мышление оперирует понятиями и силлогизмами (определенными структурами мышления, каковыми в логическом мышлении являются суждения и умозаключения).
2 из 7
В определении логического мышления, данном в словаре Современный образовательный процесс, основные понятия и термины как вида мышления, заключающегося в оперировании понятиями, суждениями и умозаключениями, перечисляются все формы, в которых такого рода мышление осуществляется [4].
А. А. Белик логическое мышление трактует как историческую форму мышления, опирающуюся на законы тождества, непротиворечивости в рассуждениях [1]. Здесь мы видим такую характеристику логического мышления, как непротиворечивость в рассуждениях.
А. А. Реан под логическим мышлением понимает вид мыслительного процесса, в котором используются логические конструкции и готовые понятия. [2].
Таким образом, сущность логического мышления заключается в следующем:
это владение совокупностью структур мышления, характеризующихся непротиворечивостью;
осуществляется в формах: понятие, суждение: умозаключение.
Коротко охарактеризуем названные формы.
Понятие – это слово (термин, которое объединяет класс объектов, обладающих некоторым набором признаков. Причем, этот набор присущ только этому классу объектов. Он называется содержанием понятия, а сам класс объектов – объемом понятия.
Пример математического понятия – прямоугольник. Этот термин объединяет все прямоугольники (например, начерченные на любой поверхности, вырезанные из какого-либо материала, существующие в представлении и т. п.). Содержанием понятия «прямоугольник» будет набор следующих признаков:
это плоская фигура,
стороны прямоугольника являются отрезками,
это многоугольник,
у него 4 вершины, 4 стороны,
3 из 7
это параллелограмм,
все углы прямые,
противоположные стороны равны,
противоположные стороны попарно параллельны,
диагонали прямоугольника равны.
Если из приведенного набора признаков выбрать необходимый и достаточный набор для распознавания прямоугольника среди других объектов, то получим определение этого понятия: «прямоугольник – это параллелограмм с прямым углом» или «прямоугольник – это четырехугольник, у которого все углы прямые».
Таким образом, над понятиями можно выполнять определенные операции, в частности, их определение, то есть формулирование набора признаков, необходимого и достаточного для распознавания этого понятия среди других объектов.
К операциям над понятиями относятся также следующие:
расширение (обобщение) понятий. Эта операция заключается в том, что из содержания понятия исключаются некоторые признаки. Так, если из содержания понятия «прямоугольник» удалить признак «углы прямые», то получим более широкое понятие «параллелограмм»;
сужение (конкретизация) понятий. Операция, обратная предыдущей. Например, добавив в содержание понятия «прямоугольник» признак «смежные стороны равны», получим более узкое понятие «квадрат» (частный случай прямоугольника);
установление отношений между понятиями. Например, отношение между понятиями «прямоугольник» и «квадрат» - родовидовые, где первое – родовое понятие, а второе – его вид.
Суждение – это повествовательное предложение, содержащее утверждение, о котором можно сказать, истинное оно или ложное. С помощью суждения связываются два понятия. Например, «квадрат – это прямоугольник». В нашем случае суждение является истинным. То есть
4 из 7
операция над суждениями заключается в установлении его истинности или ложности.
Умозаключение – это процедура перехода от одного суждения к другому. Так как суждения бывают единичными и общими, то и процедуры перехода от одного вида суждений различны.
Индукция – вид рассуждения от единичного к общему, она бывает полной (когда перебираются все единичные случаи и на основе сравнения этих случаев делается общий вывод относительно только этих случаев) и неполной (когда на основе перебора нескольких единичных суждений выявляется их сходство и делается общий вывод, фиксирующий это сходство, распространяющийся на все подобные случаи).
Приведем примеры полной и неполной индукции.
Как называется каждая из фигур? Дай общее название этим фигурам.
А1 – четырехугольник (признак В, параллелограмм;
А2 – четырехугольник (признак В, прямоугольник;
А3 – четырехугольник (признак В, квадрат;
А4 – четырехугольник (признак В).
Никаких А, кроме А1, А2, А3, А4 нет, следовательно, каждое А есть В (четырехугольник).
1. «Математика 1» (М. И. Моро)
Вычислить:
9+3 7+4 6+5
9+1+2 7+3+1 6+4+1
Объект А1 (выражение 1) имеет признак В: второе слагаемое заменяют суммой удобных слагаемых – одно из них дополняет первое число до 10.
Объект А2 (2-ое выражение) имеет признак В: второе слагаемое заменяют суммой удобных слагаемых – одно из них дополняет первое число до 10.
Объект А3 (3-е выражение) имеет признак В: второе слагаемое заменяют суммой удобных слагаемых – одно из них дополняет первое число до 10.
Следовательно, при сложении однозначных чисел с переходом через десяток (все А) второе слагаемое заменяют суммой удобных слагаемых – одно из них должно дополнять первое число до 10 (признак В).
Дедукция – это процедура перехода от общего суждения к частному. Приведем пример рассуждения ученика по дедукции.
Решить уравнение 21-х=14.
Рассуждение. В данном уравнении неизвестно вычитаемое х, уменьшаемое 21, разность равна 14. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность, В нашем случае, значит, нужно из числа 21 вычесть 14: х=21-14, х=7.
Здесь на основе общего правила нахождения неизвестного вычитаемого и анализа данного уравнения делается частный вывод о способе его решения.
Аналогия – это процедура перехода от единичного суждения к единичному. Например, ученики, сравнивая уже изученный способ сложения столбиком двузначных чисел с изучаемым способом такого же сложения трехзначных чисел, находя сходство в записи сложения и выделяя дополнительное свойство «единицы складываются с единицами, десятки складываются с десятками», делают предположительный вывод о том, что сотни складываются с сотнями (тем самым переносится способ сложения с одного разряда на другой).
Таким образом, мы видим, что выполняя действия с понятиями, суждениями, умозаключениями, обучающиеся осуществляют анализ, синтез, сравнение, обобщение и другие базовые логические действия. Следовательно, в структуре логического мышления целесообразно выделить элементы, которые отражены на рисунке.
Литература
1. Белик А. А. Культурология. Антропологические теории культур. Учебное издание /А. А. Белик. – М. : Российский гос. гуманит. ун-т., 1999. – 241 с. – – Режим доступа: https://terme.ru/slovari/kultorologija-antropologicheskie-teorii-kultur-slovar-ponjatii-i-terminov.html
2. Психология человека от рождения до смерти. — СПб. : ПРАЙМ-ЕВРОЗНАК. Под общей редакцией А. А. Реана. 2002.
3. Словарь-справочник по возрастной и педагогической психологии [Текст] : учебное пособие [Электронный ресурс] / Федеральное гос. бюджетное образовательное учреждение высш. проф. образования "Карельская гос. пед. акад. " ; сост. : Е. О. Бурачевская, Н. Ю. Скороходова. - Петрозаводск : Изд. дом ПИН, 2011. - 100 с. – Режим доступа: https://didacts.ru/slovari/slovar-po-pedagogicheskoi-psihologii.html
4. Современный образовательный процесс: основные понятия и термины : [краткий терминологический словарь] [Электронный ресурс] / М-во образования Российской Федерации, Нижнетагильская гос. социально-пед. акад., Каф. рус. яз. Каф. методики технологии и предпринимательства ; [Олешков М. Ю., Уваров В. М. ]. - Москва : Компания Спутник+, 2006. – 189 с.
– Режим доступа: https://didacts.ru/slovari/sovremennyi-obrazovatelnyi-process-osnovnye-ponjatija-i-terminy.html onjatii-i-terminov.html