![]() Ольга Ерохина
Ольга Ерохина
Развивающие игры в детском саду
▼ Скачать + Заказать документы
игра "Математический планшет"
Цель игры:
Способствовать познавательно – математическому развитию детей.
В комплект учебно-игрового пособия «Математический планшет» входят:
квадратный планшет с 25 штырьками
комплект цветных геометрических фигур (2 квадрата, 2 треугольника, 2 круга)
комплект цветных резинок
книжка с заданиями.
Развивающая игра «Прозрачный квадрат» или «Нетающие Льдинки озера Айс».
[/h4]
Прозрачный квадрат Воскобовича – это удивительная игра-головоломка, конструктор и пособие для решения логико-математических задач.
Темочки:
В набор входят 30 квадратных прозрачных пластинок с нанесенными изображениями геометрических фигур. Имеется методическая сказка «Нетающие Льдинки озера Айс, или Сказка о Прозрачном Квадрате», альбом со схемами фигурок.
В играх с «Прозрачным квадратом» необходимо соблюдать два правила:
1. При складывании квадратов пластинки накладываются друг на друга всей плоскостью.
2. При наложении пластинок друг на друга не допускается совмещение (пересечение) цветных элементов.
Развивающая игра «Квадрат Воскобовича двухцветный»
«Квадрат Воскобовича – игра-головоломка на трансформацию фигур. Выглядит он довольно просто: на квадратной основе из ткани наклеены квадраты, с одной стороны красные, с другой – зеленые.
Что развивает:
• Логическое мышление;
• Пространственное воображение;
• Конструктивные умения;
• Счетные навыки;
• Мелкую моторику руки.
Сказка – это дополнительная игровая мотивация, которая побуждает детей выполнять необходимое по сюжету действие и добиваться результата.
ТАНГРАМ - ИГРА ДЛЯ РАЗВИТИЯ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ И ФАНТАЗИИ У ДОШКОЛЬНИКОВ
Танграм— головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться между собой.
ЛОГИЧЕСКАЯ МОЗАИКА
Логическая мозаика способствует развитию воображения, логического мышления, мелкой моторики, координации движения рук и ориентировки на плоскости. С помощью игрового комплекта вы сможете уточнить представления ребенка о форме (цилиндр, диск, цвете (красный, оранжевый, желтый, зеленый, размере (высокий-низкий; выше-ниже; выше, чем, количестве (количество дисков, из которых составлены цилиндры может быть одинаковым или разным, познакомить с симметрией (слева, как справа; сверху, как снизу, развить умение мыслить, освоить логические приемы: анализ, синтез, сравнение, серизация, классификация, обобщение.
В состав нового комплекта входят 6 игровых полей красного (1 шт, оранжевого (1 шт, и желтого (4 шт) цветов. Легко скрепляющиеся между собой в большое поле и длинную дорожку. Диски 4-х цветов (диаметр 1,5 см). Всего штук – 72. При последовательном соединении одного диска с другим образуются цилиндры, которые сравниваются по высоте.
Логика и цифры
Назначение пособия состоит в освоении детьми представлений о цифре как знаке числа; умений осуществлять логические действия, выявлять отношения чисел, классифицировать. Пособие используется в качестве «жизненного материала» с целью развития логического мышления детей, как заместители блоков Дьенеша, и собственно цифры знаки в их количественном значении.
Пособие состоит из больших и маленьких цифр трех цветов: голубой, оранжевый и розовый. Игры в группах до 6 человек.
«Соты Кайе»
— это многофункциональный игровой материал, применимый для конструирования и трансформирования геометрических и образных фигур, для экспериментирования в области детского дизайна. Игра формирует у детей объемно-пространственное и ассоциативное мышление, сенсомоторные координации, помогает развивать фантазию, творческое воображение, глазомер, архитектурно-художественный вкус, чувство гармонии и композиции. Кроме того, игровой материал способствует формированию у детей таких личностных качеств, как аккуратность, сосредоточенность, усидчивость, умение работать в коллективе сверстников. Многофункциональность игрового материала позволяет проводить занятия в области математики и логики, художественного конструирования, использовать его в качестве крупной мозаики, домино и головоломки.
Данный набор состоит из 84 объёмных элементов, имеющий форму шестигранника.
«Волшебная Восьмерка 1»
Как играть с «Волшебной восьмеркой» Воскобовича
Игра имеет несколько этапов, различающихся по степени сложности. Первый этап игры– конструирование цифр по схеме. Для начала - из одноцветных деталей. Схемы приведены в методических рекомендациях к игре. Когда ребенок научится конструировать цифры можно поиграть в разнообразные игры. Например, можно показать ребенку некоторое количество предметов, а он должен в ответ не называя цифры собрать ее на игровом поле.
Когда ребенок научился собирать цифры можно осваивать и цветную сторону палочек. Расскажите ребенку о радуге и о том, что цвета в ней располагаются в определенном порядке. Можно выложить «радугу» из деталей конструктора. Затем попробуйте вместе с ребенком собрать восьмерку на игровом поле, пользуясь написанной на ней подсказкой: КОХЛЕ – красный, ОХЛЕ – оранжевый, ЖЕЛЕ - желтый, ЗЕЛЕ- зеленый, ГЕЛЕ- голубой, СЕЛЕ- синий, ФИ – фиолетовый. Освоив порядок цветов в восьмерке можно поиграть в игру «Найди ошибку». Ребенок закрывает глаза, а взрослый переворачивает несколько деталей. Ребенок должен назвать «спрятавшиеся» цвета. Или взрослый делает восьмерку неправильно, поменяв какие-то цвета местами. Ребенок должен исправить ошибки, чтобы все детали были на своих метах.
Второй этап игры – конструирование по словесной модели. Для этого нужно выучить считалку КОХЛЕ-ОХЛЕ-ЖЕЛЕ-ЗЕЛЕ-ГЕЛЕ-СЕЛЕ-ФИ. Эта считалка – шифр для создания цифры восемь. Но и остальные цифры можно зашифровать также. Например, если убрать из восьмерки голубую деталь получится цифра девять. То есть считалка для цифры девять будет КОХЛЕ-ОХЛЕ-ЖЕЛЕ-ЗЕЛЕ-СЕЛЕ-ФИ. Вместе с ребенком конструируем цифры и составляем для них шифры-считалки. Когда малыш освоит игру можно загадывать ему считалку, а он должен узнать, что за цифра зашифрована, и собрать ее. Или пусть он загадывает цифры, которые собрал Вам, называя их цветовой шифр. Чтобы было интереснее, можно загадывать, сколько спрятано игрушек или конфет или какую-нибудь другую «секретную информацию».
Третий этап игры – мысленное создание словесных моделей цифр без опоры на действие. Называем шифр любой цифры, а ребенок должен угадать цифру, не собирая ее. Или вспоминаем все цифры, в которых есть зеленая (можно загадать любой из семи цветов) деталь. Сколько их всего? Или так же вспоминаем цифры, в которых нет загаданной детали.
«Найди спрятанную цифру»
Восьмерка может превращаться в другие цифры. Я буду вам говорить какие палочки по цвету необходимо убирать, чтобы получить цифру, а вы будете выполнять.
Блоки Дьенеша
Развивающая игра блоки Дьенеша способствуют развитию логических, аналитических способностей детей. Вводятся такие первичные понятия, как логические действия, кодирование информации, структура и алгоритмы выполнения действий.
Вспомним что представляют собой блоки Дьенеша?
Логические блоки Золтана Дьенеша представляют собой набор из 48 логических блоков, различающихся четырьмя свойствами: формой – (круглые, квадратные, треугольные, прямоугольные, цветом – (красные, синие, желтые, размером – (большие и маленькие, толщиной – (толстые и тонкие).
Игровые упражнения по методике Дьенеша доступно знакомят детей с формой, цветом, размером и толщиной объектов, с математическими представлениями.
Так как блоки Дьенеша относятся к развивающим играм, то игра имеет классическую структуру.
1. Задача (задачи).
2. Дидактический материал (собственно блоки, таблицы, схемы).
3. Правила (знаки, схемы, словесные инструкция).
4. Действие, в основном, по предложенному правилу - описание, модель, таблица, схема.
5. Результат - обязательно сверяемый с поставленной задачей.
Блоки Дьенеша позволяют решать задачи образовательные, развивающие, воспитательные. Они представлены на слайде.
Образовательные:
Формировать умение выявлять в объектах разнообразные свойства, называть их;
Формировать умение обобщать объекты по одному, двум, трм, свойствам с учтом наличия или отсутствия каждого, сравнивать, анализировать, классифицировать, обобщать, абстрагировать, кодировать и декодировать информацию;
формировать представления о математических понятиях (алгоритм, кодирование и декодирование информации, кодирование со знаком отрицания);
Развивающие:
развивать сенсорные эталоны (цвет, размер) и сопоставлять предметы (по цвету, длине, ширине, высоте);
развивать познавательные процессы восприятия, памяти, внимания, мышления, воображения;
развивать творческие способности, воображение, фантазию, способности к моделированию и конструированию;
Воспитательные:
воспитывать трудолюбие, умение доводить начатое дело до конца;
воспитывать самостоятельность, инициативу, настойчивость в достижении цели.
В каких же разделах формирования элементарных математических представлений можно использовать логические блоки Дьенеша:
В разделе «количество и счет» - в работе по выявлению общих свойств отдельных предметов и групп предметов, выделению из множества отдельных его частей, по совершенствованию навыков счета и отсчета в пределах 10, по усвоению понятий поровну, не поровну, больше, меньше; в упражнениях на закрепление знаний о составе числа из единиц в пределах десяти и из двух меньших чисел. Также блоки помогут усвоить смысл арифметических действий сложения и вычитания, научить детей составлять арифметические задачи в одно действие.
В разделе «величина» - сравнение предметов по размеру (большие, маленькие, по толщине (толстые, тонкие) путем непосредственного соизмерения и сравнения на глаз.
В разделе «форма» блоки помогут углубить и расширить представления о геометрических фигурах и формах предметов. В этом разделе хорошо использовать в работе с детьми карточки-символы.
«Ориентировка в пространстве». Обучая детей ориентироваться на плоскости (умение раскладывать определенное количество фигур в указанном направлении в верхней, нижней части, слева, справа, в середине, в левом верхнем (левом нижнем, в правом верхнем (правом нижнем) углу) и так далее.
I. Ознакомительный этап.
Дети начинали освоение материала с простого манипулирования фигурами. Для этого выкладывала перед детьми наборы и давала им вволю наиграться с деталями: они начали сразу же строить различные постройки и играть с ними. В процессе исследовательской деятельности с блоками, дети установили самостоятельно, что блоки имеют различную форму, цвет, размер, толщину.
Итог работы первого этапа – выявили и закрепили знание о свойствах блоков.
II этап. Освоение умений выявлять и абстрагировать свойства предметов.
На втором этапе формировала умение детей выделять в блоках одно, а потом два свойства (цвет, форму, размер, толщину, сравнивать, классифицировать и обобщать предметы по каждому из этих свойств.
Детям предлагались разные игровые задания и упражнения.
1. Выделить блоки по двум признакам (цвету и форме, форме и размеру).
Давала задание: Найдите все такие фигуры, как эта, по цвету и форме (форме и размеру, по цвету, форме и размеру).
Найдите такие фигуры, как эта по цвету, но другой формы (такие же по форме, но другого размера).
2. Построить длинный паровозик или «цепочку» в разных вариантах.
От произвольно выбранной фигуры постройте цепочку так, чтобы рядом не было фигур одинаковых по цвету и форме (форме и размеру).
3. Игра «Волшебный мешочек».
Все фигурки складывались в мешок. Дети на ощупь доставали все круглые блоки (все большие или все толстые). Все фигурки опять же складывались в мешок.
II. Знакомство с кодовыми карточками, обозначающими свойства блоков. На втором этапе вводится специальный код, графически изображающий данные свойства:
• цвет обозначается пятном
• величина - силуэт домика (большой, маленький).
• форма - контур фигур (круглый, квадратный, прямоугольный, треугольный).
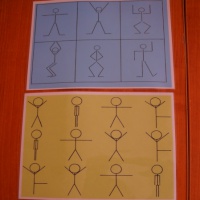
• толщина - условное изображение человеческой фигуры (толстый и тонкий).
Использование карточек позволяет развивать у детей способность к замещению и моделированию свойств, умение кодировать и декодировать информацию о них.
Работа введется следующим образом: идет выделение свойств и кодирование информации, и наоборот- ее раскодирование.
Игровые упражнения проводились так: ребенку или группе детей показывала карточку и предлагала найти все такие же блоки, назвать их. Например, на карточке обозначен синий цвет, значит нужно найти все синие фигуры, если ребенку показывала жёлтое пятно и маленький дом, нужно показать жлтую, маленькую фигуру, или (отложить все жлтые, маленькие фигуры).
Детям очень нравится игра Небылица. В игре «Небылица» Дети из блоковвыкладывали животных, используя кодовые обозначения.
После освоения этих умений можно усложнить задание. Предлагаются такие игры: "Кто быстрее соберет блоки!", "Поручения", "На свое место".
Следующий этап в работе с блоками – это освоение слов и знаков, обозначающих отсутствие свойства.
Когда дети свободно научатся пользоваться кодовыми карточками, вводится код, обозначающий знак отрицания «не» (не квадратной формы, значит круглой, или треугольной; не красный, значит синий, или желтый; не большой, значит маленький и т. д.). Работа в данном этапе по формированию понимания отрицания свойств проводится постепенно.
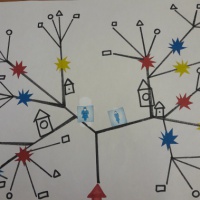
Использовала игры «Помоги фигуркам выбраться из леса». В ней сначала устанавливали, для чего на разветвлении дорог расставлены знаки.
Ориентировались в пространстве, озвучивая, куда идут – вправо или влево.
Сейчас формирую у детей умение оперировать одновременно двумя свойствами отрицания.
Например, в игре «Гирлянда» формирую умение раскладывать блоки в обручи в соответствии с указанными свойствами. В зелёный обруч не кладем не синих и не квадратных.
Вариантом логических игр для детей подготовительной группы являются игры с обручами. Ведущий кладет на пол обруч, обводит указкой то место, которое находится внутри обруча, и добавляет, что вся остальная часть пола находится вне обруча.
Игра с одним обручем
Правила игры: на полу лежит обруч. У каждого ребенка в руке один блок. Дети по очереди располагают блоки в соответствии с заданием ведущего. Например, внутри обруча - все красные блоки, а вне обруча - все остальные. Детям задают вопросы: Какие блоки лежат внутри обруча? (Красные). Какие блоки оказались вне обруча? (Не красные). Верен именно такой ответ, т. к. важно лишь то, что внутри обруча лежат все красные блоки и никаких других там нет. Усложненный вариант – игра с двумя обручами
Кубики Сложи узор
Игра состоит из 16 кубиков, грани которых окрашены в четыре цвета (красный, желтый, синий, белый) определенным образом. С помощью этой игры можно развить у ребенка пространственное воображение, аккуратность, внимание, графические способности, а также умение анализировать, синтезировать, комбинировать.
В игре с кубиками дети выполняют три разных вида заданий:
- учатся по узорам-заданиям складывать точно такой же узор из кубиков;
- ставится обратная задача: глядя на кубики, сделать рисунок узора, который они образуют.
- придумывать новые узоры из девяти или 16 кубиков, каких еще нет в книге, т. е. выполнять уже творческую работу. Используя разное число кубиков и разную не только по цвету, но и по форме (квадраты и треугольники) окраску кубиков, можно изменять сложность заданий в достаточно широком диапазоне.
Варианты игры: 1. Выкладывать узор из 16 кубиков.
2. Выкладывать узор по образцу.
3. Выкладывать узор по образцу на время.
4. Выкладывать узор, используя творческое воображение
Игра «Сложи квадрат»
Цель: - закрепить представления о сенсорных эталонах цвета и формы, соотношении целого и части;
- развивать сообразительность, пространственное воображение, логическое мышление, математические и творческие способности;
- учитьразбивать сложное задание на несколько простых, создавая алгоритм действияв игре;
- способствовать развитию таких черт характера как сосредоточенность, внимательность, находчивость, упорство в достижении цели.
Варианты игры 1. Сложите квадраты в рамках по цветам, назовите их цвет и форму деталей, из которых они состоят.
2. Сложите квадраты в рамках, следуя порядку цветов в солнечном спектре (радуге): красный, оранжевый, желтый и т. д.
3. Сложите квадраты в два столбика: отдельно «теплые», отдельно «холодные».
4. Сложите квадраты не в рамках, а на столе, на полу. Лишенные степени свободы, они хуже складываются.
5. Сложите квадраты на скорость, как можно быстрее, соревнуясь друг с другом.
6. Предварительно отобрав нужные детали, сложите квадрат или несколько с закрытыми глазами.
7. Сложите квадраты из деталей разного цвета.
8. Сложите квадраты из различных деталей игр «Сложи квадрат» разных уровней сложности.
9. Составьте по расчлененной схеме фигуру-картинку, подобрав нужные части квадратов, назовите получившуюся фигуру.
Волшебный поясок
Версия известной во всем мире игры «ДА-НЕТКА» для детей 4-8 лет. Данная игра учит точно задавать вопросы и попутно развивает другие интеллектуальные умения: наблюдать, видеть проблему, выдвигать гипотезу, давать определения понятиям, сравнивать, структурировать, классифицировать, наблюдать, делать выводы, доказывать и защищать идеи.
Этот метод дает возможность научить детей находить существенный признак в предмете, классифицировать предметы и явления по общим признакам, слушать и слышать ответы других, строить на их основе свои вопросы, точно формулировать свои мысли.
1. Игровое поле – пояс с десятью кармашками.
2. Пять комплектов тематических картинок (“Геометрические фигуры”, “Часы”, “Грибы”, “Животные”, “Транспорт”).
3. Две прищепки, выполняющие функции меток (для сужения поля поиска).
4. Фишки.
Правила игры:
• Карточки из одного комплекта, например “Домашние животные” раскладываются по кармашкам в пояске. Один из игроков назначается ведущим.
• Ведущий задумывает одно из животных, изображенное на карточке. Другие игроки должны отгадать задуманный предмет, задавая наводящие вопросы, на которые ведущий может отвечать только “Да” или “Нет”.
В кармашки можно выкладывать картинки не только из одного тематического набора, можно составлять свои комплекты с картами разных тем.
Прищепки используются для сужения поиска картинки. Например игрок может спросить: карта находится справа или слева от прищепки, тем самым облегчая себе поиск.
Производители рекомендуют помечать картинки, выбранные ведущим, дабы исключить споров, какая же картинка первоначально была задумана.
Примерный ход игры:
На столе раскладываются картинки из разных тематик: животные домашние, дикие, мебель…
Игрок: Это животное с фермы?
Ведущий: да
Игрок: Это птица?
Ведущий: Нет
Игрок: У животного есть мех?
Ведущий: Нет
Игрок: у животного есть рога?
Ведущий: Да
Игрок: Это корова!
ЦВЕТНЫЕ СЧЕТНЫЕ ПАЛОЧКИ КЮИЗЕНЕРА
Каждая палочка – это число, выраженное цветом и величиной. С математической точки зрения палочки это множество, на котором легко обнаруживаются отношения эквивалентности и порядка. В этом множестве скрыты многочисленные математические ситуации. Цвет и величина, моделируя число, подводят детей к пониманию различных абстрактных понятий, возникающих в мышлении ребенка естественно как результат его самостоятельной практической деятельности.
Использование «чисел в цвете» позволяет одновременно развить у детей представление о числе на основе счета и измерения. К выводу, что число появляется на основе счета и измерения, дети приходят на базе практической деятельности, в результате разнообразных упражнений.
С помощью цветных палочек детей также легко подвести к осознанию отношений больше-меньше, больше-меньше на, научить делить целое на части и измерять объекты условными мерками, поупражнять в запоминании состава чисел из единиц и меньших чисел, подойти вплотную к сложению, умножению, вычитанию и делению чисел.
Кроме этого, играя с палочками, дети осваивают такие понятия как «левое», «длинное», «между», «каждый», «одна из…», «какой-нибудь», «быть одного и того же цвета», «быть не голубого цвета», «иметь одинаковую длину» и др.
Комплект состоит из 116 пластмассовых призм 10-ти различных цветов и форм. Наименьшая призма имеет длину 10 мм и является кубом.
Выбор цвета преследует цель облегчить использование комплекта. Палочки 2,4,8 образуют «красную семью», 3,6,9 – «синюю семью». «Семейство желтых» составляют 5 и 10. Подбор палочек в одно семейство (класс) происходит не случайно, а связан с определенным соотношением их по величине. Например, в семейство красных входят числа кратные двум и т. д.
В каждом из наборов действует правило: чем больше длина палочки, тем больше значение того числа, которое она выражает.
Игра "Геоконт"
Игра "Геоконт" развивает сенсорику, мелкую моторику, логику, фантазию, учит силуэтному конструированию, совершенствует интеллект и развивает творческие и логические способности ребенка. Согласно определенным заданиям, ребенок натягивает резинки на гвоздики так, что создает предметные силуэты, геометрические фигуры, узоры, цифры, буквы - по образцу, словесному алгоритму и собственному замыслу.
В пособии к игре-конструктору «Геоконт» по методике Воскобовича есть разные описания схематических рисунков, которые должны получаться в результате работы. Эта игра помогает детям раннего возраста: ознакомиться с азами геометрии (дать понятие и разъяснение определенным геометрическим фигурам и их особенностям); развить мелкую моторику, которая непрерывно связана с речевыми способностями; строить геометрические фигуры по картинке или схеме, воспринимая информацию на слух или же самостоятельно составив схему у себя в воображении; ознакомиться с основными цветами, формами, величинами.
Для старших детей Геоконт по методике Воскобовича помогает строить схемы по образцу, учиться моделировать, изучать систему координат и уметь ориентироваться в ней. Также эта игра способствует развитию разных способностей: навыков нестандартного мышления; формированию внимания, памяти, креативного мышления; умению быстро искать схожесть и различия между предметами, рисунками; становлению психологических аспектов развития.
Игра «Геовизор»
«Геовизор» представляет собой альбом 15*21 см и состоит из двух листов. Верхний - это прозрачная пленка с нанесенной координатной сеткой, подобной игровому полю «Геоконта». На пленке имеются отверстия на направляющих стрелках и нижний-подложка (картон).
Как играть.
1. Рисуем под диктовку отрезками.
Взрослый называет координаты (точки) отрезков, составляющих фигуру. Дети отмечают маркером две точки одного отрезка (например, Ф4-Ф2) и проводят его. Аналогично рисуют следующий отрезок (например, Ф2-К2) и так далее, до полного построения фигуры.
При необходимости изображение можно перенести на подложку или лист бумаги.
2. Рисуем по образцу.
Дети рисуют фигуру по образцу, который создается на листе бумаги с координатной сеткой «Геовизора» или игре «Геоконт».
Занятия с «Геовизором» Воскобовича дают представления о пространственных отношениях, количественном счете, симметрии, системе координат, делении целого на равные и неравные части. Ребенок развивает умение решать логико-математические задачи, внимание, память, мышление, воображение и творческие способности, мелкую моторику руки.
«Чудо крестики 2»
Ребенок решает головоломку, знакомится с цветами и геометрическими фигурами, из частей головоломки складывает различные фигуры, развивая логическое мышление, моторику рук, конструкторские способности и воображение.
Ребенок сначала складывает "крестики" непосредственно в рамке или на столе, а затем конструирует фигуры по схемам из альбома (с различными уровнями сложности) или по собственному замыслу.
Можно собирать и накладывать крестики один на другой.
Игры можно усложнять перевернув все крестики цветной стороной вниз.