Нина Шилова
Кроссворд «Математическая шкатулка» для учащихся 8–9 классов
▼ Скачать + Заказать документы
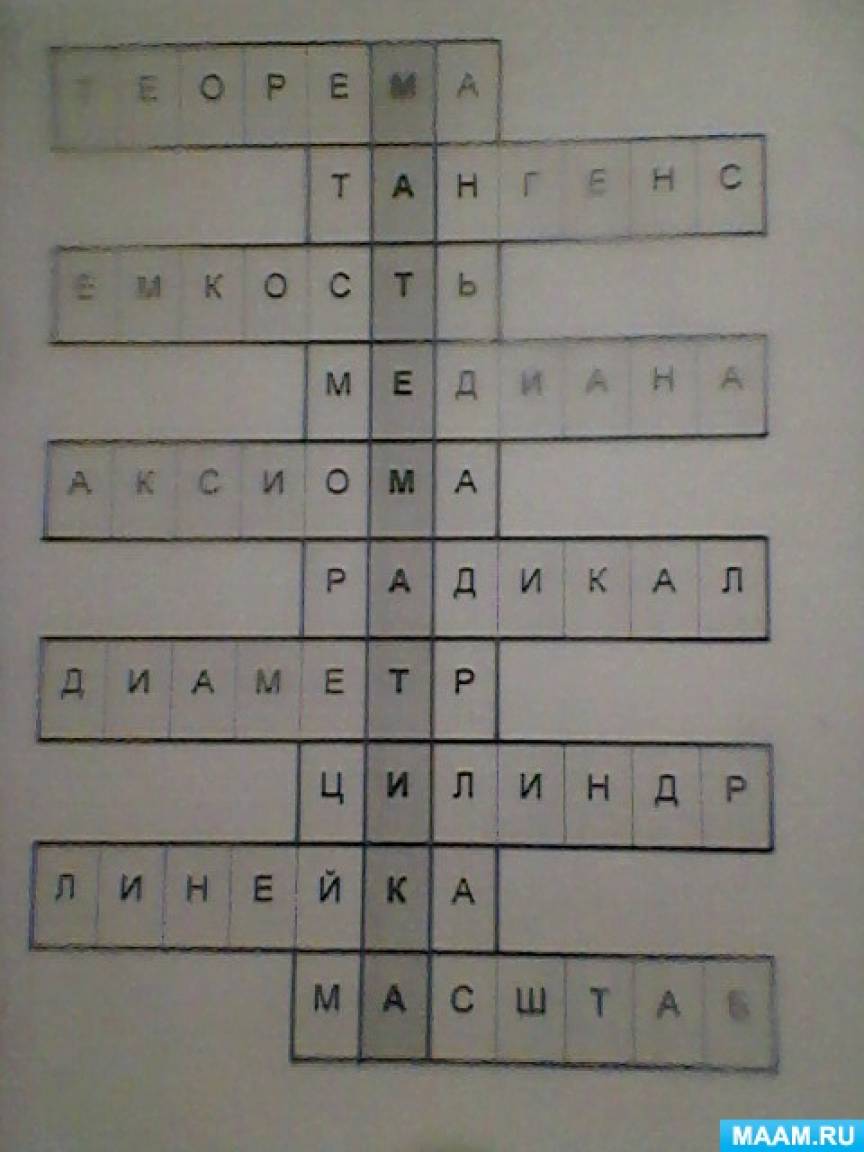
Кроссворд «Математическая шкатулка»
Кроссворд «Математическая шкатулка» составлен для школьников 8-9 классов с целью проверки их умения ориентироваться в разных разделах математики. Цель: вызвать интерес к изучению математики, способствовать формированию логического мышления у школьников, чтобы они стали интеллектуально развитыми людьми и заняли достойное место в нашем обществе в будущем.
По горизонтали:
Публикация «Кроссворд „Математическая шкатулка“ для учащихся 8–9 классов» размещена в разделах
- Кроссворды для детей
- Математика. Конспекты уроков
- Средняя школа, 8 класс
- Средняя школа, 9 класс
- Средняя школа. 5-9 классы
- Школа. Материалы для школьных педагогов
- Темочки
- Конкурс для воспитателей и педагогов «Лучшая авторская дидактическая игра» декабрь 2019
1. Утверждение, требующее доказательства с помощью других теорем и общепринятых утверждений, аксиом.
2. Одна из тригонометрических функций угла прямоугольного треугольника.
3. Внутренний объем сосуда.
4. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
5. Утверждение, принятое без доказательства.
6. Знак извлечения квадратного корня.
7. Отрезок, соединяющий две точки на окружности и проходящий через её центр.
8. Фигура, которая получается в результате вращения прямоугольника вокруг своей стороны.
9. Простейшее средство измерений, представляющее собой узкую пластину, у которой как минимум одна сторона прямая и имеет нанесённые штрихи (деления, кратные единице измерения длины.
10. Отношение размера изображения к размеру изображаемого объекта.
По вертикали:
11. Если все слова по горизонтали будут записаны правильно, то в колонке под №11 (по вертикали) получится название точной науки о количественных отношениях и пространственных формах действительного мира, которую «уже затем учить надо, что она ум в порядок приводит», по высказыванию М. В. Ломоносова.
Ответы на кроссворд «Математическая шкатулка» (8-9 кл.)
По горизонтали:
1. Утверждение, правильность которого требуется доказать с помощью рассуждений. (требующее доказательства) (Теорема)
2. Одна из тригонометрических функций угла прямоугольного треугольника (Тангенс).
3. Внутренний объем сосуда (Емкость).
4. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны (Медиана).
5. Утверждение, принятое без доказательства (Аксиома).
6. Знак извлечения квадратного корня (Радикал).
7. Отрезок, соединяющий две точки на окружности и проходящий через её центр (Диаметр).
8. Фигура, которая получается в результате вращения прямоугольника вокруг своей стороны (Цилиндр).
9. Простейшее средство измерений, представляющее собой узкую пластину, у которой как минимум одна сторона прямая и имеет нанесённые штрихи (деления, кратные единице измерения длины (Линейка).
10. Отношение размера изображения к размеру изображаемого объекта (Масштаб).
По вертикали:
11. Если все слова по горизонтали будут записаны правильно, то в колонке под №11 (по вертикали) получится название точной науки о количественных отношениях и пространственных формах действительного мира, которую «уже затем учить надо, что она ум в порядок приводит», по высказыванию М. В. Ломоносова (Математика): «Математику уже затем учить надо, что она ум в порядок приводит».
