![]() Жанна Бубнович
Жанна Бубнович
Логико-математическое развития дошкольников 5–7 лет «Знакомство с графами»
Логико-математическое развитие дошкольников 5-7 лет : знакомство с графами.
Уважаемые коллеги, сегодня я хочу Вас познакомить с методикой, направленной на развитие логико-математических представлений о математических свойствах и отношениях предметов через такое понятие как «теория графов». Граф - абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин. Логико-математическое развитие дошкольников предполагает формирование таких мыслительных умений и способностей, которые позволяют легко осваивать новое, развивать гибкость мышления, учить логике, формировать память, внимание, воображение и речь.
Публикация «Логико-математическое развития дошкольников 5–7 лет „Знакомство с графами“» размещена в разделах
- Консультации для педагогов и воспитателей
- Математика. Математические представления, ФЭМП
- Развитие детей. Материалы для педагогов
- Темочки
- Конкурс для воспитателей и педагогов «Лучшая методическая разработка» октябрь 2020
Всем нам известно, что игра это ведущий вид деятельности детей дошкольного возраста, в ходе которой дети овладевают умением вести поиск решения самостоятельно. Воспитатель лишь вооружает детей схемой и направлением анализа задачи, приводящего в конечном результате к решению. Самые простые не требуют ни умения считать, ни знания букв. Эти упражнения очень хорошо развивают пространственное мышление.
Материалы, используемые на занятиях:
- яркие и красочные карточки с изображением, подобранные по понятиям: животные, птицы, овощи, фрукты, посуда, мебель, одежда, игрушки и др. ;
- цветные карандаши;
- игровые поля размером А3 (город, зоопарк, деревня);
- песочница;
- небольшие фигурки персонажей и игрушечных машинок;
- атласные ленты и шнуры.
Система работы с детьми проходит в 4 этапа:
- подготовительный этап - знакомство с графами;
- обучение изображению натуральных объектов разноцветными точками («Разноцветные точки»);
- обучение изображению объектов одноцветными, но разновеликими точками («Разновеликие точки»);
- формирование ещё более высокой степени абстрагирования мышления детей от конкретных предметов и явлений («Однородные множества»).
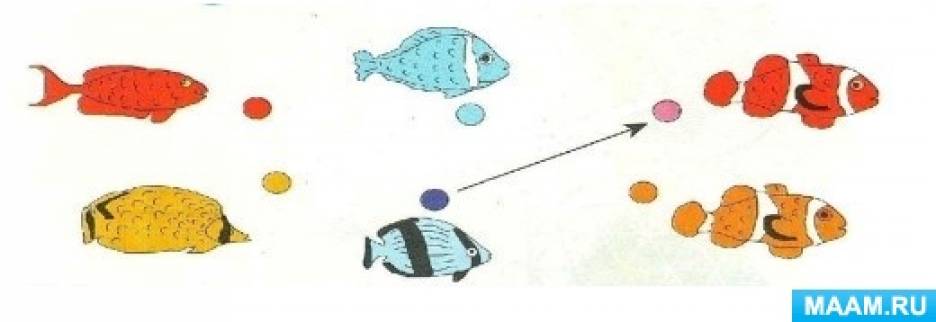
1. На подготовительном этапе дети знакомятся с понятием «граф». Дошкольникам предлагаются задания на зрительное восприятие и внимательность. Раздаются карточки, на которых изображены множества и предлагается отобразить последовательность действий. Пример: на рисунке изображены плывущие рыбки. Внизу листа под каждой рыбкой изображен кружек определенного цвета (рис. 1). На другой карточке необходимо обозначить последовательность, какая рыбка плывет первой, какая второй и т. д. (рис. 2).
Детям дается пояснение, что такое обозначение на картинках называется графами. Точки при этом называются вершинами, а линии – ребрами графа.
Рис. 1. Плывущие рыбки.
Рис. 2. Обозначить последовательность плывущих рыбок.
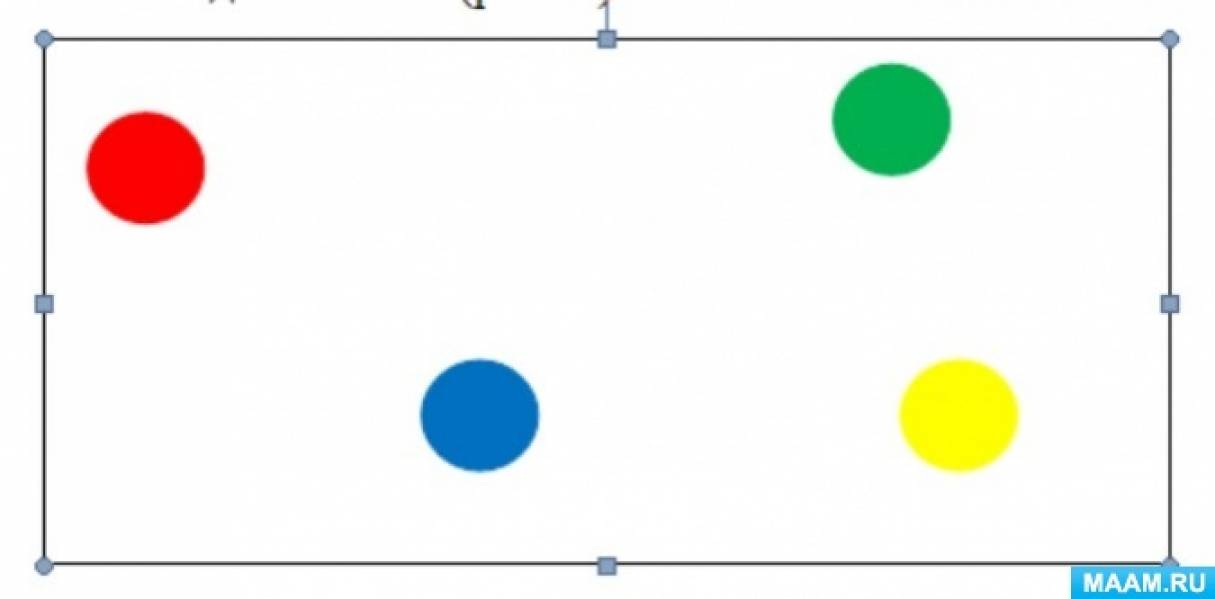
2. На втором этапе происходит обучение изображению натуральных объектов «разноцветными точками». Дошкольникам рассказывается игровая проблемная ситуация: например, почтальон приносит телеграмму, в которой сообщается, что к детскому саду приближается злой колдун с другой планеты и хочет забрать всех с собой. Необходимо спрятать ваших членов семьи, чтобы злой колдун не смог никого найти. Чтобы это сделать, надо «превратить» каждого члена семьи в цветную точку. Эту точку нарисовать в рамке на любом месте. Колдун никого не узнает, а мы-то знаем, кто спрятан за каждой точкой (рис. 3).
Рис. 3. Разноцветные точки.
Далее педагог просит детей ответить на вопросы: кто спрятан за красной точкой? Жёлтой? Зелёной? И т. д. Как можно назвать множество точек в рамке? (Множество членов семьи.) Предлагается узнать и назвать каждый элемент этого множества.
Для упражнения детей в полученном навыке можно дать задание изобразить различные множества при помощи разноцветных точек ( множество съедобных грибов: красная точка - подосиновик, коричневая - боровик, жёлтая - лисичка, серая - сыроежка; множество овощей: красная точка - помидор, зелёная - огурец, коричневая - картофель, оранжевая - морковь и т. д.). Игры, используемые для закрепления материала «Подарок», «Бывает – не бывает».
Графами с цветными точками можно моделировать ситуации различных сказок: «Теремок», «Колобок», «Репка», «Дом, который построил Джек», «Королевский бутерброд», «Петушок и бобовое зёрнышко» и др.
3. На третьем этапе происходит переход от обучения изображению натуральных объектов разноцветными точками к обучению изображению объектов одноцветными, но «разновеликими точками». На первых занятиях может быть то же изображение членов семьи, но исполнение его должно быть несколько иным. Детям предлагается изобразить кружки-точки разного размера, но одинакового цвета. Под самым большим кругом «спрятать» папу, под средним кружком – маму, под маленьким кружком – себя и так далее (рис. 4).
Рис. 4. Разновеликие точки.
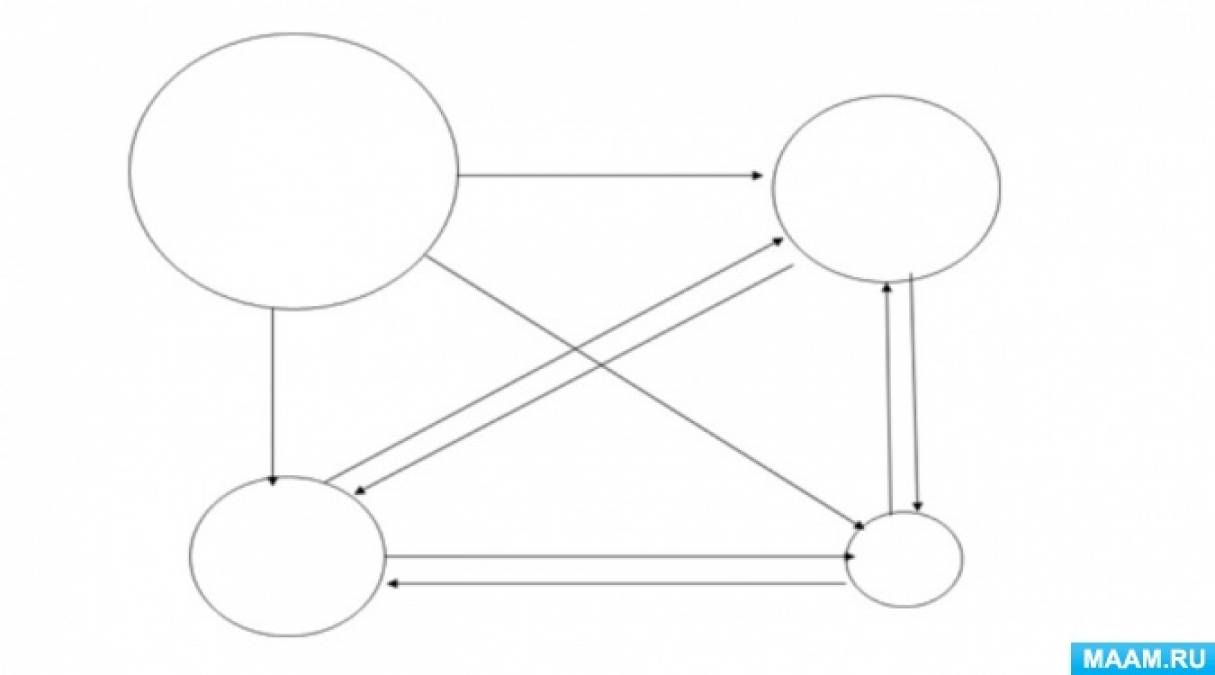
Аналогичная работа может проводиться с однородными и разнородными предметными множествами. Использование стрелок в обозначении последовательности упражняет детей в сериации.
Для закрепления знаний можно поиграть в игры «Готовим угощения», «Собери в корзину», «Так - не так». Цель игр: упражнять детей в установлении действий по заранее заданному графическому изображению множества (графу); формировать элементы логического, схематического мышления.
4. На последнем этапе происходит формирование ещё более высокой степени абстрагирования мышления детей от конкретных предметов и явлений. Работа ведётся на «однородных множествах», элементы которых обозначаются либо чёрными точками на бумаге, либо белыми - мелом на доске. Каждая точка называется предметом - элементом представленного множества. Графическое изображение множества может использоваться не только для показа отношений между элементами внутри множества, но и для показа образования числа, для обучения вариативным способам соотнесения элементов двух (трёх) множеств.
Для обучения вариативным способам соотнесения элементов двух множеств можно использовать графы, в которых элементы сначала представляются как стилизованные изображения, а затем как разноцветные или разновеликие точки.
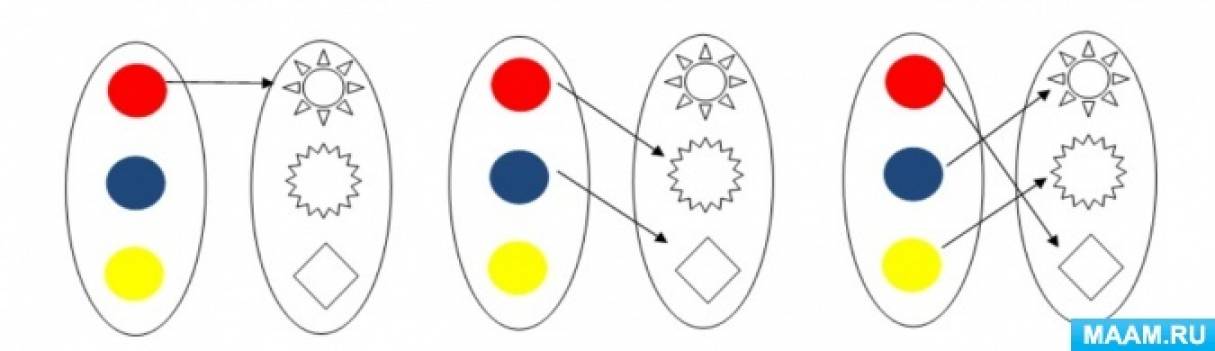
Детям рассказывается история, в конце ставится проблема, разрешение которой предлагается детям. Например, в сюжетном занятии о цветах педагог рассказывает, о том, что в гостях у Феи цветов были три гномика: в красной шапочке, в синей и в жёлтой. Они помогали Фее раскрашивать цветы разными красками. За хорошую работу она решила их наградить выращенными цветами. У Феи на клумбах были ромашки, колокольчики, гвоздики. Она предложила каждому гному взять с каждой клумбы по одному цветку и сделать себе букеты, в которых будет по 3 цветка: 1 ромашка, 1 колокольчик, 1 гвоздика.
Детям необходимо помочь гномам. Нужно нарисовать 3 пары овалов. В графах слева рисуются точки: красная точка – гномик в красной шапочке, синяя – в синей шапочке и жёлтая – гномик в жёлтой шапочке. В графах справа – цветы : - ромашка,
- гвоздика, - колокольчик.
Стрелками показываем гномика и цветок, который он взял с каждой клумбы. Следим, чтобы в букете у каждого гномика цветы не повторялись (рис. 5).
Рис. 5. Награждение гномов цветами.
В процесс обучения включаются упражнения и специальные игры, позволяющие выполнить операции объединения, пересечения, нахождения разности множеств. Эти игры выполняются на полях «Путешествие по зоопарку» (рис. 6, «Путешествие по сказке», «Путешествие по городу» (рис. 7, «Путешествие по морю», «Путешествие по космосу», «Что где растет - кто где живет» (рис. 8).
Ребра графа дети выкладывают лентами и шнурами. В играх могут быть заданы проблемные ситуации – на дороге ремонт, нужно найти другой путь и пассажирский маршрут. А так же очень увлекательным для детей будет игра на песке с использованием миниатюрных фигурок-героев сказок.
Рис. 6. Путешествие по зоопарку.

Рис. 7. Путешествие по городу.

Рис. 8. Что где растет - кто где живет.


Вывод: Таким образом, применение в образовательном процессе логико-математических игр с использованием графов способствует развитию пространственной ориентировке дошкольников, развивает гибкость мышления, воображение, речь, коммуникативные навыки, умение осваивать новое, решать нетиповые поисковые развивающие проблемные ситуации.
Список литературы:
1. Журнал для дошкольников «Кораблик» №84 Ирина Житко.
2. https://ideas4parents.ru Блок Ксении Несютиной. Математика без счета и цифр: возможно ли это?